この記事は Google 翻訳を使用して処理されました
問題の説明
回路基板の上端と下端には n 個の端子があります。回路設計によれば、$(i, \pi(i))$ は、上側の端子 i と下側の端子 $\pi(i)$ の間の接続を表すために使用され、これは回路図上の i 番目の接続と呼ばれます。
下の図に示す $\pi(i)$ は、任意の $1 \le i < j \le n $ に対して ${8, 7, 4, 2, 5, 1, 9, 3, 10, 6}$ として配置されます。i 番目のリンクと j 番目のリンクが交差するための必要十分条件は $\pi(i)>\pi(j)$ である。
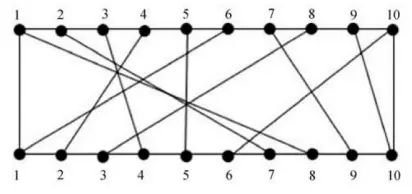
回路基板を作るとき、これらのn本の配線を複数の絶縁層に分配する必要があり、同じ層の配線は交差しません。次に、どの配線を層に配置するかを決定する必要があります。このレイヤーで可能な限り多くのリンク、つまりリンクセット $Nets={ (i,\pi(i)),1\le i\le n }$ の最大の分離サブセットを決定する。
問題分析
$N(i,j)={ t|(t,\pi(t))\in Nets, t\le i, \pi(t) \le j }$ とする。$N(i,j)$ の最大の分離部分集合を $MNS(i,j)$ ，$size(i,j)=|MNS(i,j)|$ とする。
分析の結果、この問題は最適なサブ構造特性を持つことがわかりました。規模 n の回路配線問題では、次の再帰式を構築できます。
$$ \begin{align*} &(1) \ \ i=1\ とする、 size(1,j)= \begin{cases} 0, & \text{j<$\pi$(1)} \ 1, & \text{その他の状況} \end{cases} \ &(2) \ \ i>1\ とする， size(i,j)= \begin{cases} size(i-1,j), & \text{j<$\pi$(i)} \ max{size(i-1,j),size(i-1,\pi(i)-1)+1}, & \text{その他の状況} \end{cases} \end{align*} $$
C コード
#include <stdio.h>
#include <stdlib.h>
#define N 10 // 問題の大きさ
// 分離した接続の最大数を見つける
void maxNum(int pi[], int **size);
// 最大分離接続セットを構築します。net[i]は、最大分離サブセット内のi番目の接続の上位端末のシリアル番号を表します。
int constructSet(int pi[], int **size, int *net);
int main(void){
// 下付き文字は1から始まります
int pi[N+1] = {0, 8, 7, 4, 2, 5, 1, 9, 3, 10, 6};
int net[N];
int **size;
size = (int**)malloc(sizeof(int*)*(N+1));
for(int i=0;i<N+1;i++)
size[i]=(int*)malloc(sizeof(int)*(N+1));
maxNum(pi, size);
int m = constructSet(pi, size, net);
printf("分離接続の最大数は次のとおりです。%d\n",m);
printf("含まれる接続は次のとおりです。\n");
for(int i=0; i<m; i++){
printf("(%d,%d)\n", net[i], pi[net[i]]);
}
}
void maxNum(int pi[], int **size){
// size[i][j]: 上部と下部にそれぞれ i と j の端子がある回路基板の最初の層における分離接続の最大数
int i,j;
// when j<pi(1)
for(j=0; j<pi[1]; j++)
size[1][j];
// when j>=pi(1)
for(j=pi[1]; j<=N; j++)
size[1][j];
for(i=2; i<N; i++){
// when j<pi(i)
for(j=0; j<pi[i]; j++)
size[i][j] = size[i-1][j];
// when j>=c[i]
for(j=pi[i]; j<=N; j++)
size[i][j]=size[i-1][j]>=size[i-1][pi[i]-1]+1 ? size[i-1][j] : size[i-1][pi[i]-1]+1;
}
// 最大接続数
size[N][N] = size[N-1][N]>=size[N-1][pi[N]-1]+1 ? size[N-1][N] : size[N-1][pi[N]-1]+1;
}
// 最大分離接続セットを構築します。net[i]は、最大分離サブセット内のi番目の接続の上位端末のシリアル番号を表します。
int constructSet(int pi[], int **size, int *net){
int i;
int j=N;
int m=0; // 端末セット内の最大接続数を記録する
for(i=N; i>1; i--){ // 減少
// (i,pi[i])は最大の互いに素な部分集合を結ぶ線である。
if(size[i][j] != size[i-1][j]){
net[m++]=i; // iを配列ネットに記録し、接続ラインの数を1増やす
j=pi[i]-1; // 拡張リンクバー間隔を更新しました
}
}
// when i=1
if(j>=pi[1])
net[m++] = 1;
return m;
}
その他のコンテンツ
検索中に既存の記事が見つかりました： 算法设计与分析——电路布线（动态规划）