📢 This article was translated by gemini-3-flash-preview
Problem Description
A circuit board has $n$ terminals on both the top and bottom sides. According to the circuit design, $(i, \pi(i))$ represents a connection between the top terminal $i$ and the bottom terminal $\pi(i)$, referred to as the $i$-th net.
The $\pi(i)$ permutation shown below is $\{8, 7, 4, 2, 5, 1, 9, 3, 10, 6\}$. For any $1 \le i < j \le n$, net $i$ and net $j$ intersect if and only if $\pi(i) > \pi(j)$.
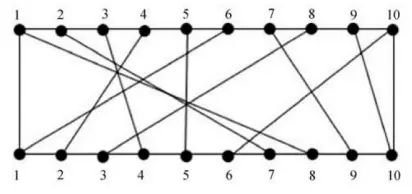
When manufacturing the circuit board, these $n$ nets must be distributed across multiple insulating layers. Nets on the same layer must not intersect. We need to determine which nets to place on a single layer to maximize the total number of connections. This means finding the Maximum Non-crossing Subset (MNS) of the set $Nets=\{ (i,\pi(i)), 1 \le i \le n \}$.
Problem Analysis
Let $N(i,j)=\{ t \mid (t,\pi(t)) \in Nets, t \le i, \pi(t) \le j \}$. The maximum non-crossing subset of $N(i,j)$ is $MNS(i,j)$, and its size is $size(i,j) = |MNS(i,j)|$.
Analysis shows that this problem exhibits optimal substructure. For a circuit routing problem of size $n$, we can construct the following recurrence:
$$
\begin{align*}
&(1) \ \text{When } i=1, \\
&size(1,j)= \begin{cases}
0, & \text{j < } \pi(1) \\
1, & \text{otherwise}
\end{cases}
\\
&(2) \ \text{When } i>1, \\
&size(i,j)= \begin{cases}
size(i-1,j), & \text{j < } \pi(i) \\
\max\{size(i-1,j), size(i-1,\pi(i)-1)+1\}, & \text{otherwise}
\end{cases}
\end{align*}
$$C Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
| #include <stdio.h>
#include <stdlib.h>
#define N 10 // Problem size
// Calculate the maximum number of non-crossing connections
void maxNum(int pi[], int **size);
// Construct the maximum non-crossing subset; net[i] stores the top terminal index
int constructSet(int pi[], int **size, int *net);
int main(void){
// Index starts from 1
int pi[N+1] = {0, 8, 7, 4, 2, 5, 1, 9, 3, 10, 6};
int net[N];
int **size;
size = (int**)malloc(sizeof(int*)*(N+1));
for(int i=0; i<N+1; i++)
size[i]=(int*)malloc(sizeof(int)*(N+1));
maxNum(pi, size);
int m = constructSet(pi, size, net);
printf("Maximum non-crossing connections: %d\n", m);
printf("Nets included:\n");
for(int i=0; i<m; i++){
printf("(%d,%d)\n", net[i], pi[net[i]]);
}
return 0;
}
void maxNum(int pi[], int **size){
// size[i][j]: max non-crossing connections for board with i top and j bottom terminals
int i, j;
// case when i=1
for(j=0; j<pi[1]; j++)
size[1][j] = 0;
for(j=pi[1]; j<=N; j++)
size[1][j] = 1;
for(i=2; i<N; i++){
// when j < pi(i)
for(j=0; j<pi[i]; j++)
size[i][j] = size[i-1][j];
// when j >= pi(i)
for(j=pi[i]; j<=N; j++)
size[i][j] = size[i-1][j] >= size[i-1][pi[i]-1]+1 ? size[i-1][j] : size[i-1][pi[i]-1]+1;
}
// Maximum connections at size[N][N]
size[N][N] = size[N-1][N] >= size[N-1][pi[N]-1]+1 ? size[N-1][N] : size[N-1][pi[N]-1]+1;
}
// Construct the MNS set, net[i] stores the top terminal index
int constructSet(int pi[], int **size, int *net){
int i;
int j = N;
int m = 0; // Counter for connections in the MNS
for(i=N; i>1; i--){
// If the size changed, (i, pi[i]) is part of the subset
if(size[i][j] != size[i-1][j]){
net[m++] = i; // Record i, increment count
j = pi[i] - 1; // Update the bottom terminal range limit
}
}
// handle when i=1
if(j >= pi[1])
net[m++] = 1;
return m;
}
|
Others
While searching, I came across an existing article:
Algorithm Design and Analysis — Circuit Routing (Dynamic Programming)
References
LaTeX Formula Handbook
Using LaTeX in Typora: Left-aligning multi-line formulas
Three methods to dynamically allocate a 2D array using malloc
